经纬度

纬线与纬度

纬度.png
所有纬线自成一个圆圈，被称为纬线圈，纬线圈的长度不等，最长的是赤道，由赤道向两极逐渐缩短，到两极缩成一个点。纬线指示东西方向，所有的纬线都平行，赤道把地球平分为南北两个半球。
纬度从赤道算起，把赤道定为0度，由赤道到北极和南极各分作90度，赤道以北是北纬，代号是Ｎ；以南是南纬，代号是Ｓ，北纬90度是北极，南纬90度是南极。南纬和北纬的分界线是赤道。
特殊的纬线：
0度纬线：即赤道，是最长的纬线，南北半球的分界线。
30度纬线：低、中纬度的分界线。
60度纬线：中、高纬度的分界线。
90度纬线：即南北极点，北纬90度是北极点，南纬90度是南极点。
23.5度纬线：回归线，是热带和温带的分界线，有无太阳直射现象的分界线。北纬23.5度是北回归线，南纬 23.5度是南回归线。
66.5度纬线：极圈，是温带和寒带的分界线，有无极昼和极夜现象的分界线。北纬66.5度是北极圈，南纬66.5度是南极圈。
地球是自西向东转的，箭头的方向是东，相反的方向是西。面对地图，上北下南，左西右东。

经线与经度

纬度.png
所有经线都是半圆形，经线长度都相等，经线指示南北方向，所有的经线都在南北两极点处相交，两条正对的经线组成一个经线圈，它们的度数和是180度，任何一个经线圈都可以把地球平分为两个半球。
国际上规定，把通过英国伦敦格林尼治天文台原址的那一条经线定为0度经线，也叫本初子午线。从本初子午线向东、向西，各分作180度，以东的180度属于东经，以西的180度属于西经，经度最大是180度，180度经线只有一条。东西经的分界线是0度经线和180度经线。
特殊的经线：
0度经线：即本初子午线，是东西经的分界线，以东是东经，以西是西经。
180度经线：是东西经的分界线，以东是西经，以西为东经。
西经20度经线：东西半球的分界线，以东是东半球，以西是西半球。
东经160度经线：东西半球的分界线，以东是西半球，以西是东半球。

地理位置应用

1.查询一段距离内的位置

2.根据距离排序且显示所有距离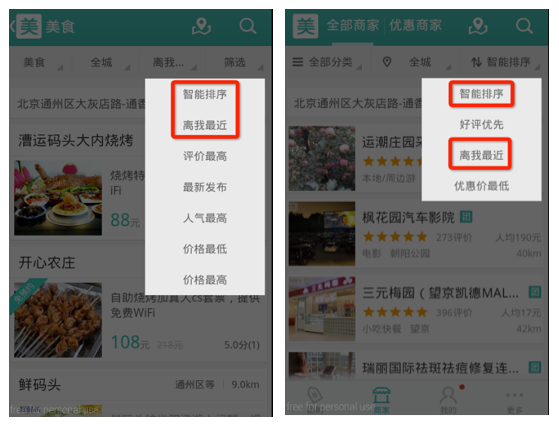
按距离排序.png

地理位置算法

GeoHash算法

划分区域至二进制

经纬度划分

GeoHash算法可以将一个二维的经纬度坐标转换成一个可比较的字符串信息，也就是一个降维的过程。具体的实现过程如下：
谷歌地图：39.1785816935,117.4612203712 (不同地图供应商所提供定位信息有差异)
纬度 latitude ：39.1785816935
经度 longitude：117.4612203712
将经纬度进行二分法的形式落于相对应的区间中，步骤如下图：39.17858169坐落于0-90的区间内，坐落于0-45的区间内，坐落于22.5-45的区间内，层层二分，数据分的越细，获取到的精度越准确；

纬度范围	划分区间0	划分区间1	39.1785816935
（-90，90）	（-90,0]	(0,90]	1
(0,90)	(0,45]	(45,90]	0
(0,45)	(0,22.5]	(22.5,45]	1
(22.5,45)	(22.5,37.5]	(37.5,45]	1
…	…	…	…

经度范围	划分区间0	划分区间1	117.4612203712
（-180，180）	（-180,0]	(0,180]	1
（0，180）	（0,90]	(90，180]	1
(90，180)	(90,135]	(135,180]	0
(90,135)	(90,112.5]	(112.5,135]	1
(112.5,135)	(112.5,123.75]	(123.75,135]	0
…	…	…	…

最终获得纬度的二进制：101101…
经度的二进制：11010…
将经纬度的二进制数进行组合，以奇数为纬度，偶数为经度组合；
经纬度组合后：111001110001…

Redis GEO

将三维转为二维

地球纬度区间是[-90,90],经度区间是[-180,180]。将它展开想象长一个矩形为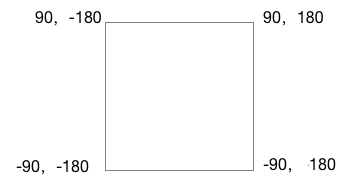
三维转二维.png

将二维转为一维

通过刚才的方法，我们能够将地球的表面转换成二维空间的平面。那接下来要将二维转变成一维。如果切割二维空间，可以切割出很多正方形。如何表示这个正方形呢？最简单的方法是在平面上进行遍历。每遍历到一个点，就给它标注一个值，比如00、01、10、11，随着二进制数字增加，相当于遍历面上不同的位置。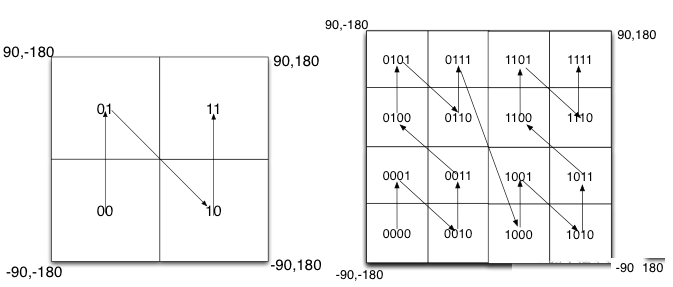
二维变一维.png
当将空间划分为四块时候，编码的顺序分别是左下角00，左上角01，右下脚10，右上角11，也就是类似于Z的曲线。
当我们递归的将各个块分解成更小的子块时可以标识更小的空间范围（如上图二中所示），如从0000开始到1111结束编码的顺序是自相似的（分形），每一个子快也形成Z曲线，这种类型的曲线被称为Peano空间填充曲线。

将二进制编码

在开发中，Base32、Base64加密解密相信大家都有遇到过和了解过，GeoHash将二维经纬度转换成可比较字符串的过程也就是一个转Base32的过程，Base32是由数据0~9及26个英文字母(减去’a’ , ’i’ , ’l’ , ’o’四个字符)

Base32

private static final char[] toBase64 = {
    '0', '1', '2', '3', '4', '5', '6', '7', '8', '9',
    'b', 'c', 'd', 'e', 'f', 'g', 'h', 'j', 'k', 'm',
    'n', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z' 
};

Base64

private static final char[] toBase64 = {
    'A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M',
    'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z',
    'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm',
    'n', 'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z',
    '0', '1', '2', '3', '4', '5', '6', '7', '8', '9', '+', '/'
};

Base32对应的二进制序列是5位，Base64对应的二进制序列是6位，我们需要将这个经纬度二进制序列转换成Base32的形式输出，将二进制序列每5位一组进行拆分得到：
11100 11100 01…..
11100转换成十进制得到 12^4 + 12^3 + 1*2^2 = 16 + 8 + 4 = 28 将28转换成Base32得到“W”
所以上面的这个二进制序列可以得到的字符串是 ww,所表示的区域范围是：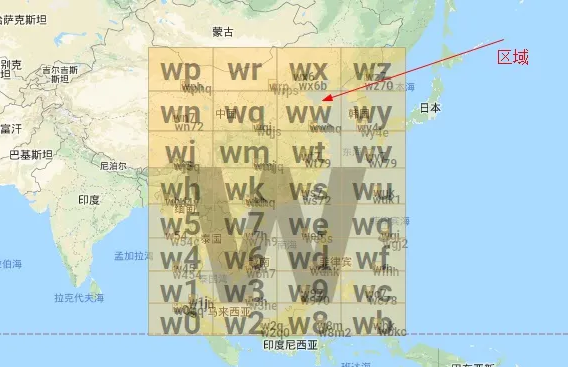

将经纬度转换成二进制序列的过程中，转换的次数越多，所表示的精度越细，标识的范围越小，我们日常生活中所描述的用户定位，在宏观上形容的并不是一个点，而是表示的一块区域信息，我们位于某一个区域范围内。

编码表示距离远近

GeoHash的位数表示距离的远近，比如，1km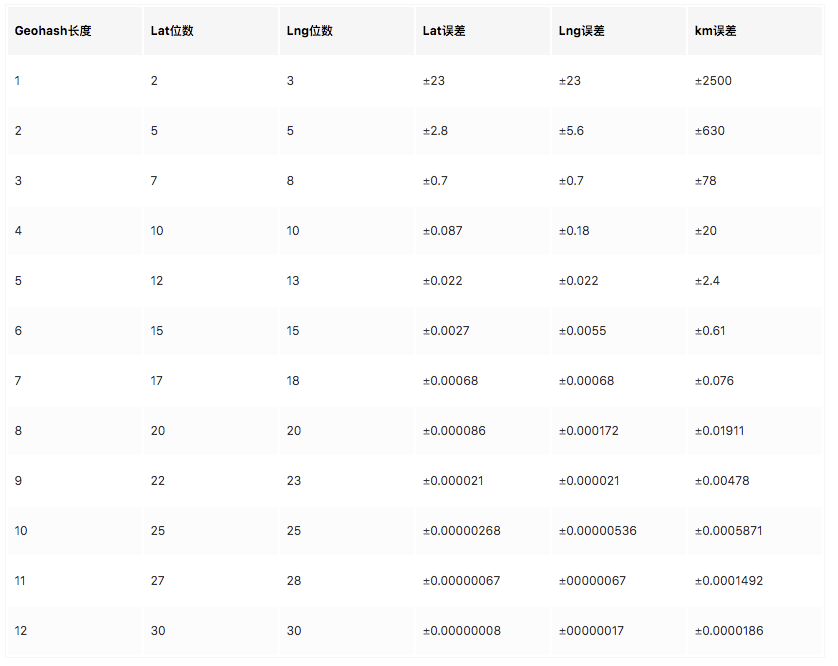
geo长度范围.png
如要查询1000m,可以使用5位编码。过滤掉大部分的人，然后再进行距离计算。

GeoHash算法问题

如下图所示，根据可比较字符串来划分区域，会存在一个边界问题；
geo算法比较.png
解决的思路很简单，我们查询时，除了使用定位点的GeoHash编码进行匹配外，还使用周围8个区域的GeoHash编码，这样可以避免这个问题。

距离计算

Haversine公式

public static double distHaversineRAD(double lat1, double lon1, double lat2, double lon2) {
        double hsinX = Math.sin((lon1 - lon2) * 0.5);
        double hsinY = Math.sin((lat1 - lat2) * 0.5);
        double h = hsinY * hsinY +
                (Math.cos(lat1) * Math.cos(lat2) * hsinX * hsinX);
        return 2 * Math.atan2(Math.sqrt(h), Math.sqrt(1 - h)) * 6367000;
    }

目前北京地区在线服务有5w个POI，计算一遍距离需要7ms。现在数据增长特别快，未来北京地区POI数目增大到100w时，我们筛选服务仅计算距离这一项就需要消耗144多ms，性能十分堪忧。（注：本文测试环境的处理器为2.9GHz Intel Core i7，内存为8GB 1600 MHz DDR3，操作系统为OS X10.8.3，实验在单线程环境下运行）

POI数目	耗时（ms）
5w	7
10w	14
100w	144

简化算法

public static double distanceSimplify(double lat1, double lng1, double lat2, double lng2, double[] a) {
     double dx = lng1 - lng2; // 经度差值
     double dy = lat1 - lat2; // 纬度差值
     double b = (lat1 + lat2) / 2.0; // 平均纬度
     double Lx = toRadians(dx) * 6367000.0* Math.cos(toRadians(b)); // 东西距离
     double Ly = 6367000.0 * toRadians(dy); // 南北距离
     return Math.sqrt(Lx * Lx + Ly * Ly);  // 用平面的矩形对角距离公式计算总距离
    }
}

POI数目	耗时（ms）
5w	0.5
10w	1.1
100w	11

进一步简化算法

public static double[] trainPolyFit(int degree, int Length){
    PolynomialCurveFitter polynomialCurveFitter = PolynomialCurveFitter.create(degree);
    double minLat = 10.0; //中国最低纬度
    double maxLat = 60.0; //中国最高纬度
    double interv = (maxLat - minLat) / (double)Length;
    List<WeightedObservedPoint> weightedObservedPoints = new ArrayList<WeightedObservedPoint>();
    for(int i = 0; i < Length; i++) {
        WeightedObservedPoint weightedObservedPoint = new WeightedObservedPoint(1,  minLat + (double)i*interv, Math.cos(toRadians(x[i])));
        weightedObservedPoints.add(weightedObservedPoint); 
    }
    return polynomialCurveFitter.fit(weightedObservedPoints);
}


public static double distanceSimplifyMore(double lat1, double lng1, double lat2, double lng2, double[] a) {
     //1) 计算三个参数
     double dx = lng1 - lng2; // 经度差值
     double dy = lat1 - lat2; // 纬度差值
     double b = (lat1 + lat2) / 2.0; // 平均纬度
     //2) 计算东西方向距离和南北方向距离(单位：米)，东西距离采用三阶多项式
     double Lx = (a[3] * b*b*b  + a[2]* b*b  +a[1] * b + a[0] ) * toRadians(dx) * 6367000.0; // 东西距离
     double Ly = 6367000.0 * toRadians(dy); // 南北距离
     //3) 用平面的矩形对角距离公式计算总距离
     return Math.sqrt(Lx * Lx + Ly * Ly);
}

POI数目	耗时（ms）
5w	0.1
10w	0.3
100w	4

基础知识

#GeoHash #RedisGeo #Haversine公式 #经纬度

距离计算

http://byj.zzmd.tech/2023/06/08/距离计算/

作者

白玉京

发布于

2023年6月8日

许可协议

锁的机制下一篇